Giải thuật sắp xếp: Quick sort

Xin chào, Tui là Hiếu đây :). Hôm nay tôi lại mạn phép được viết thêm 1 xíu về 1 loại thuật toán sắp xếp đã ra đời rất rất lâu rồi, đó là Quick sort.

Quick sort là gì?

Quick sort là một trong những thuật toán sắp xếp nhanh và hiệu quả nhất, nó được phát triển bởi Tony Hoare vào năm 1959.

Thuật toán này thực hiện trên nguyên tắc chia để trị để sắp xếp các phần tử trong 1 mảng. Phương pháp này chia mảng ban đầu thành 2 mảng con, mảng đầu tiên sẽ chứa các phần tử nhỏ hơn hoặc bằng với phần tử "pivot" (ở đây mình sẽ lựa chọn ngẫu nhiên trong mảng ban đầu), và mảng còn lại sẽ chứa các phần tử lớn hơn phần tử pivot. Sau đó sử dụng đệ quy để tiếp tục thao tác trên các mảng con đó, với mục đích là đem pivot về đúng vị trí của nó.

Quick sort hoạt động như thế nào?

Nghe những gì mình diễn giải bằng lời phía trên chắc khó hiểu lắm nhỉ (mình đọc lại cũng hem hiểu luôn 🙈🙈)?

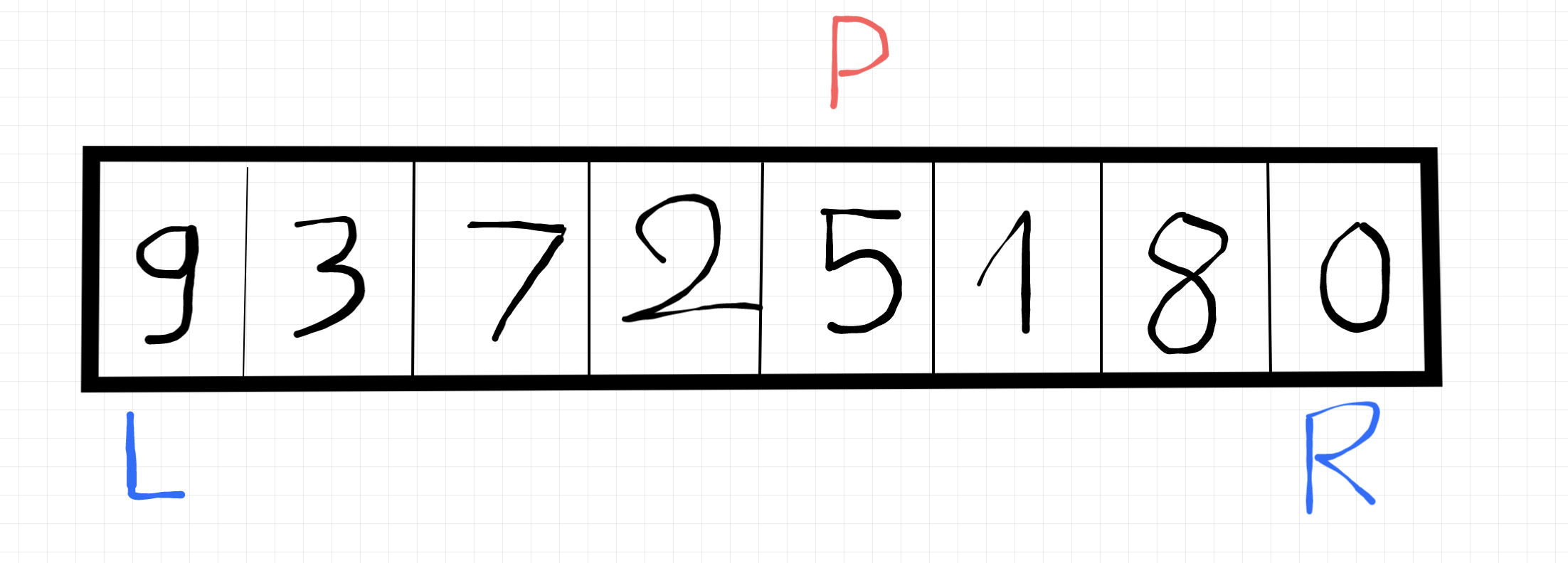
Ví dụ: Chúng ta có 1 mảng đầu vào như thế này 🤔

[9,3,7,2,5,1,8,0]

Một điều luôn nhớ là:

• Tất cả các phần tử bên phải pivot phải lớn hơn pivot
• Tất cả các phần tử bên trái pivot phải nhỏ hơn pivot.

Mình sẽ chọn ngẫu nhiên pivot là 5 (mình thích chọn ngẫu nhiên thôi), phần tử left sẽ ở vị trí thứ 0 của mảng là số 9 và phần tử right sẽ ở vị trí cuối cùng của mảng có giá trị là 0.

• So sánh pivot và right, 5 có bé hơn 0 không nhỉ? Tất nhiên là không rồi, vậy chúng ta sẽ hoán vị 5 và 0 🙃

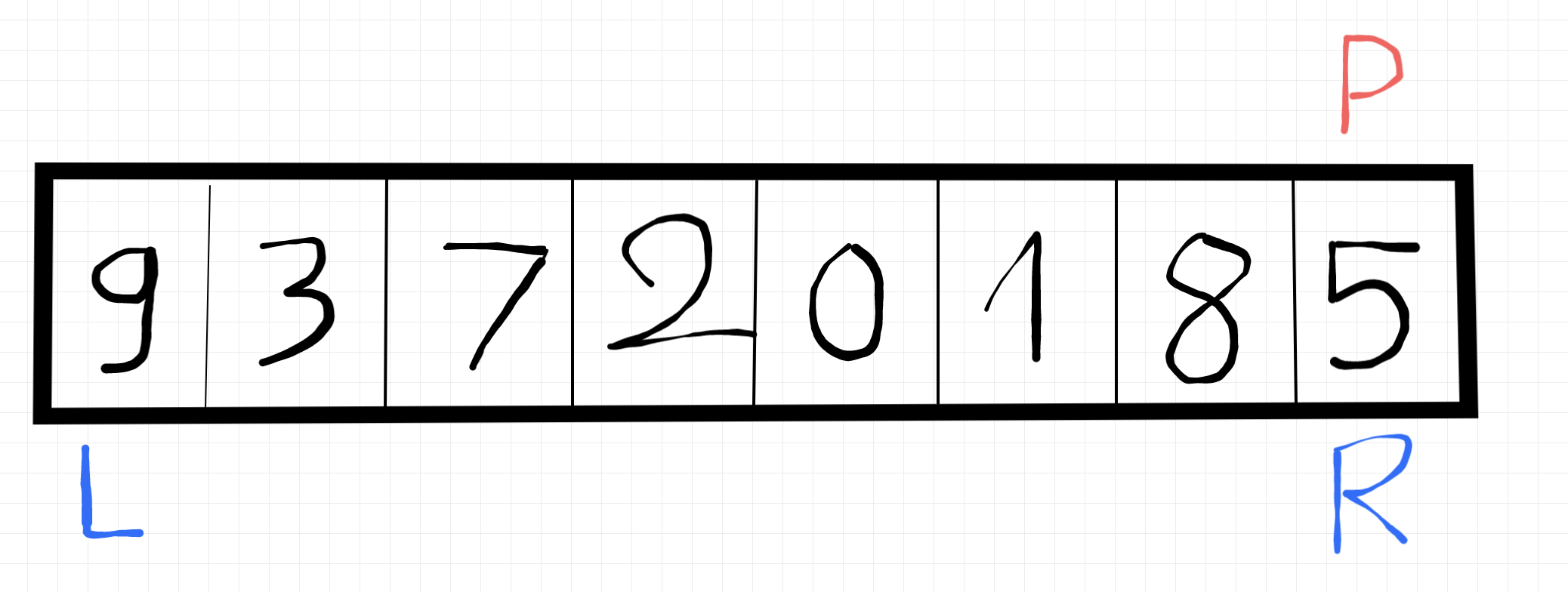
Lúc này pivot sẽ nằm ở vị trí right, nên chúng ta sẽ bắt đầu so sánh tại vị trí left là 9 nhé.
Chắc chắn là 5 không lớn hơn 9, thế nên ta sẽ hoán vị pivot và left 🙃, và vị trí của pivot lúc này sẽ di chuyển về left.

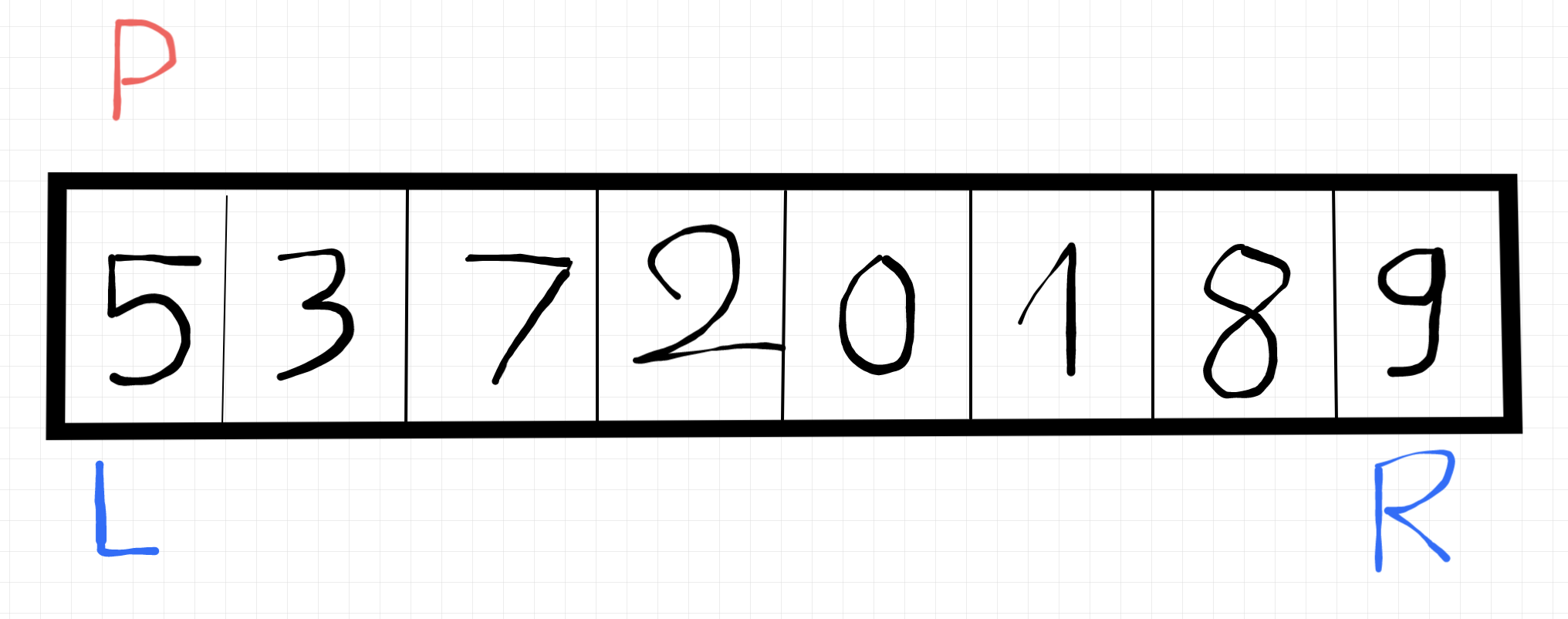
Vì lúc này pivot đã nằm tại left, nên chúng ta sẽ tiếp tục so sánh tại right nè. 5 có bé hơn số 9 không? Có nhé, thế nên vị trí right sẽ lùi về 1 - tức là số 8.

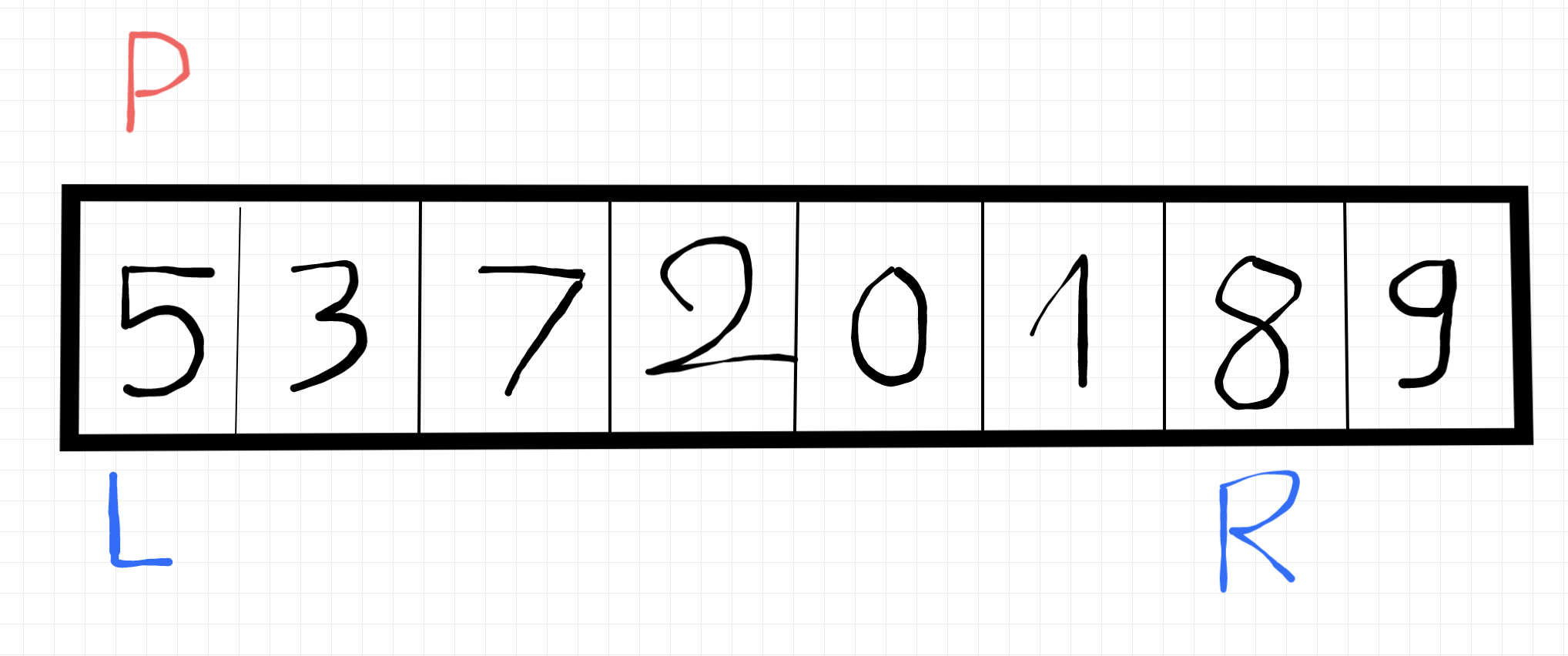
Lặp lại, so sánh 5 và 8 ta thấy 5 bé hơn 8 thế là tiếp tục lùi vị trí right xuống 1, lúc này sẽ mang giá trị là 1.

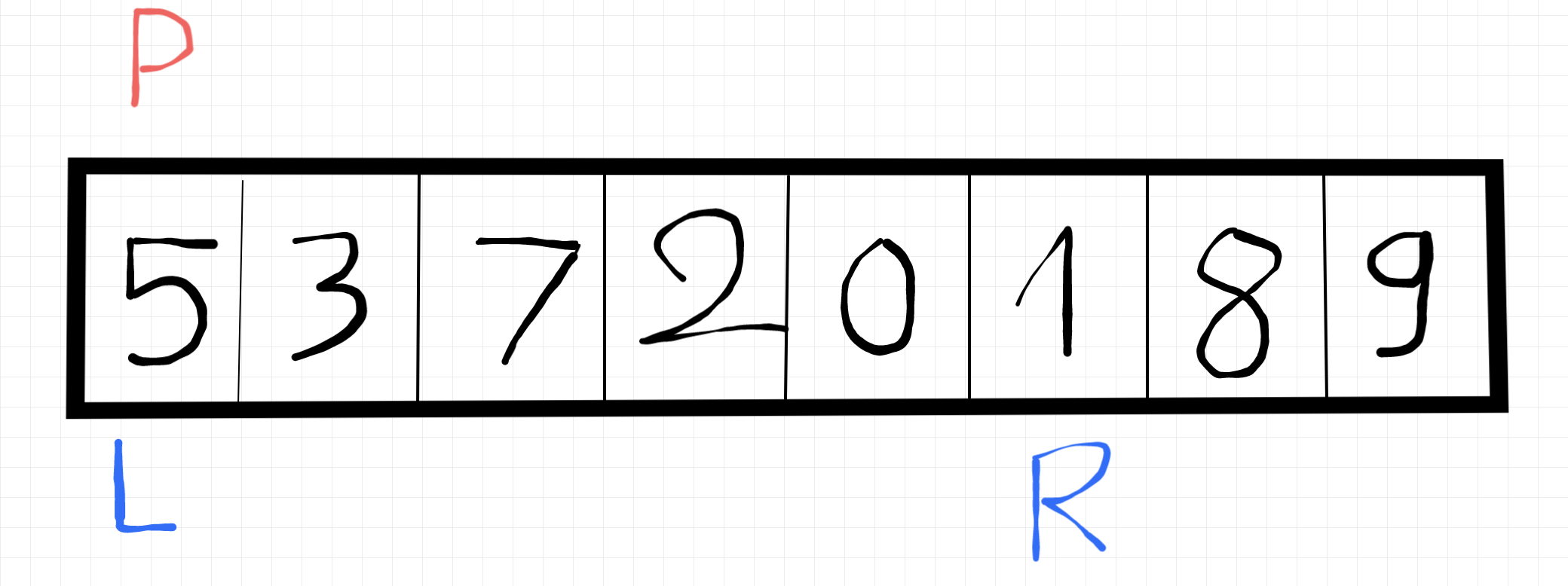
Tiếp tục so sánh nào, kiểm tra xem pivot (5) có bé hơn right (1) không. Kết luận là có vậy là ta sẽ tiếp tục hoán vị pivot và right.

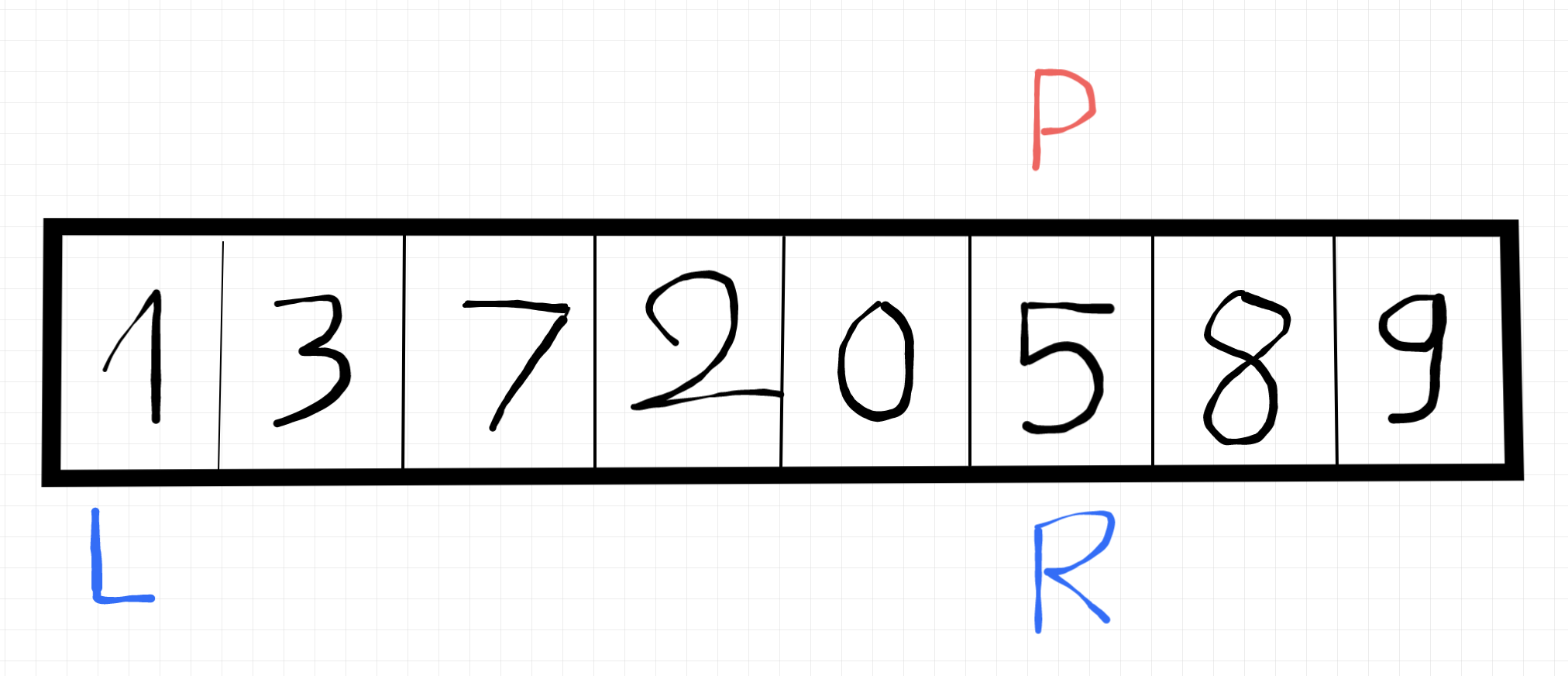
Quen chưa quen chưa, các bạn đã quen với các bước làm chưa? Chưa thì tiếp nhé, Lúc này pivot đã nằm ở vị trí right, nên ta sẽ so sánh với left (trái phải trái phải 🥹). 5 sẽ lớn hơn 1 nên tăng vị trí left lên 1 - lúc này có giá trị là 3

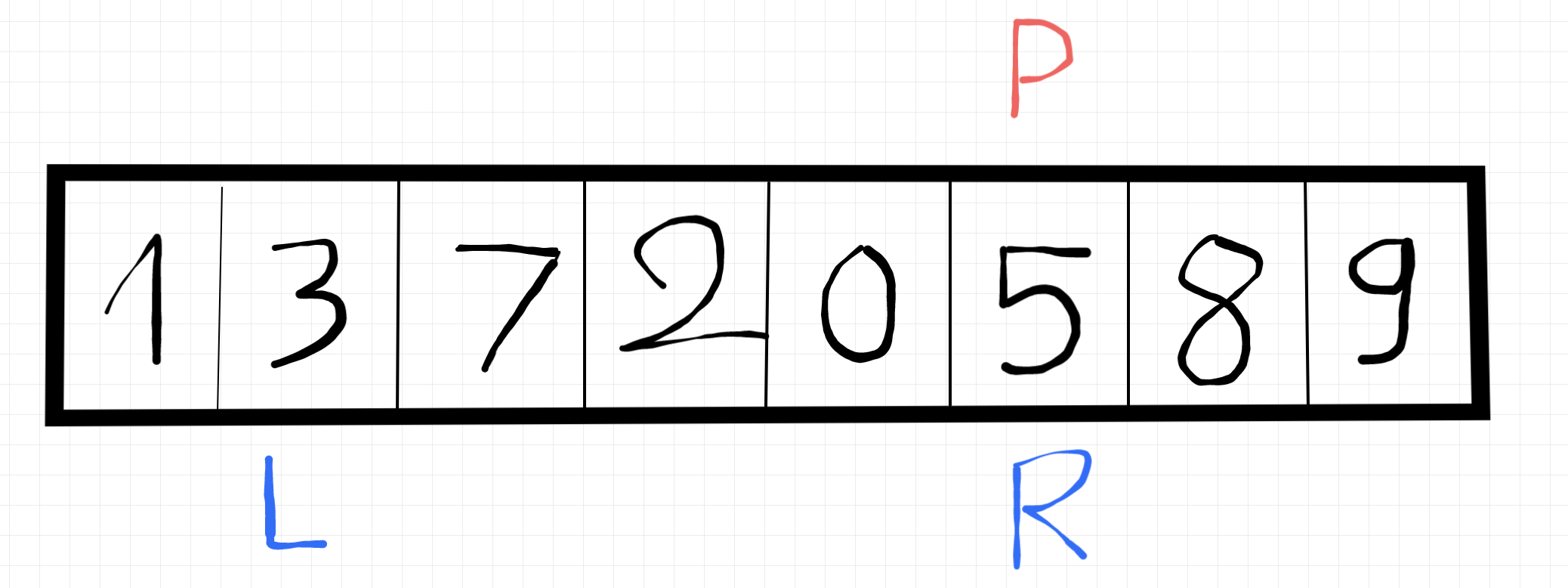
So sánh 5 và 3 thì ta có 5 lơn hơn 3, ok rối nhé, tiếp tục dịch left lên 1.

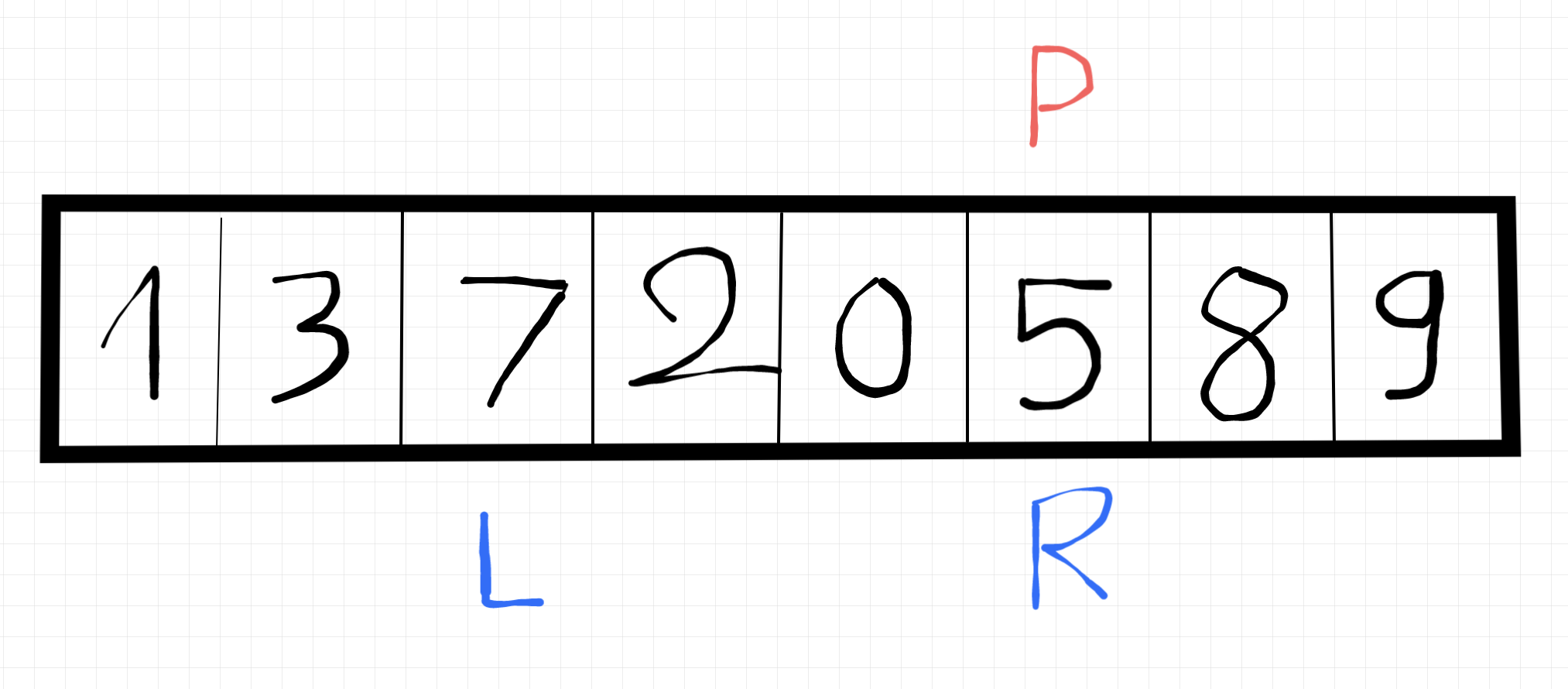
Tại đây ta so sánh pivot và left, 5 bé hơn 7, swap gấp 🙃, và dời pivot về vị trí left

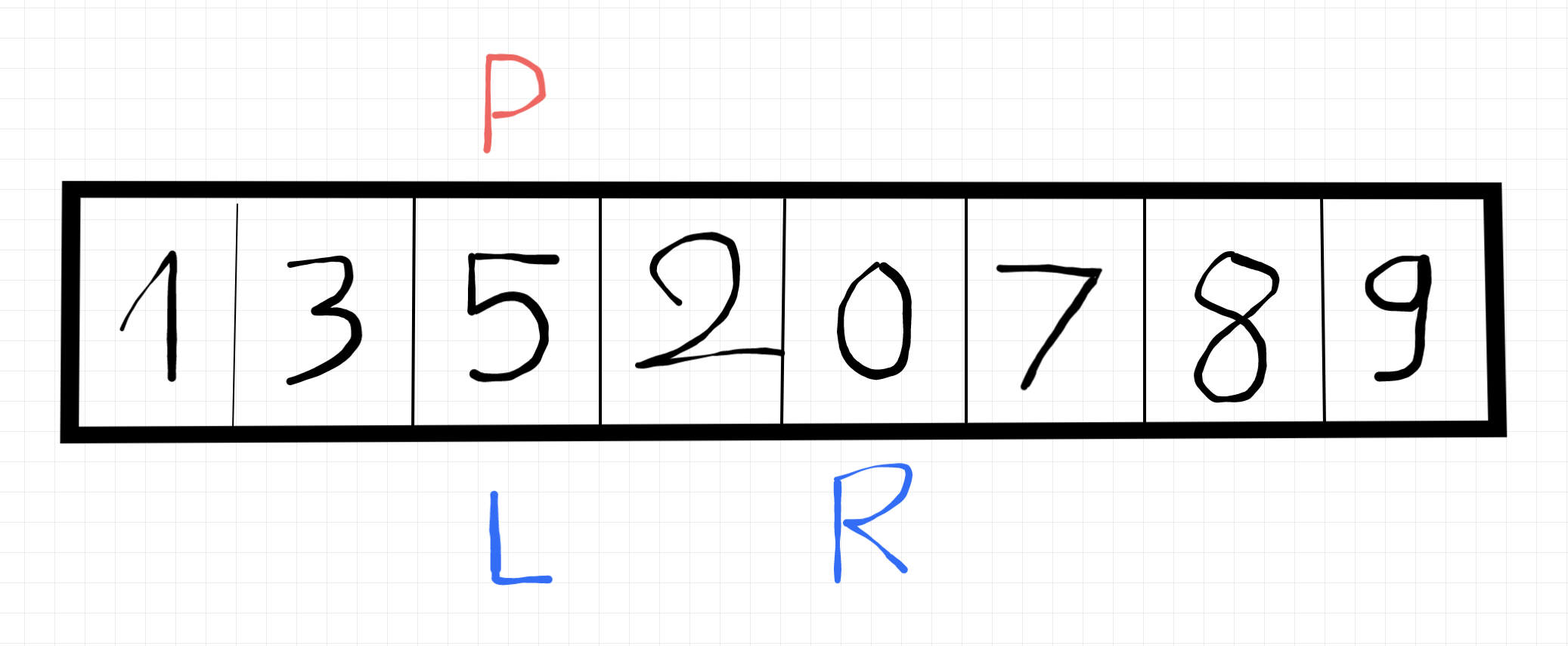
Ok quen hơn chưa các bạn, mình lấy ví dụ hơi dài, xin lỗi 🥲. làm nhanh nhé, so sánh pivot lúc này nằm ở vị trí left với right (7), 5 thì bé hơn 7, nên vị trí right sẽ lùi xuống 1 vị trí, nên tight lúc này mang giá trị là 0. Tiếp tục so sánh, 5 và 0 (hình như so sánh rồi). hoán vị 🙃 và dời pivot đến right.

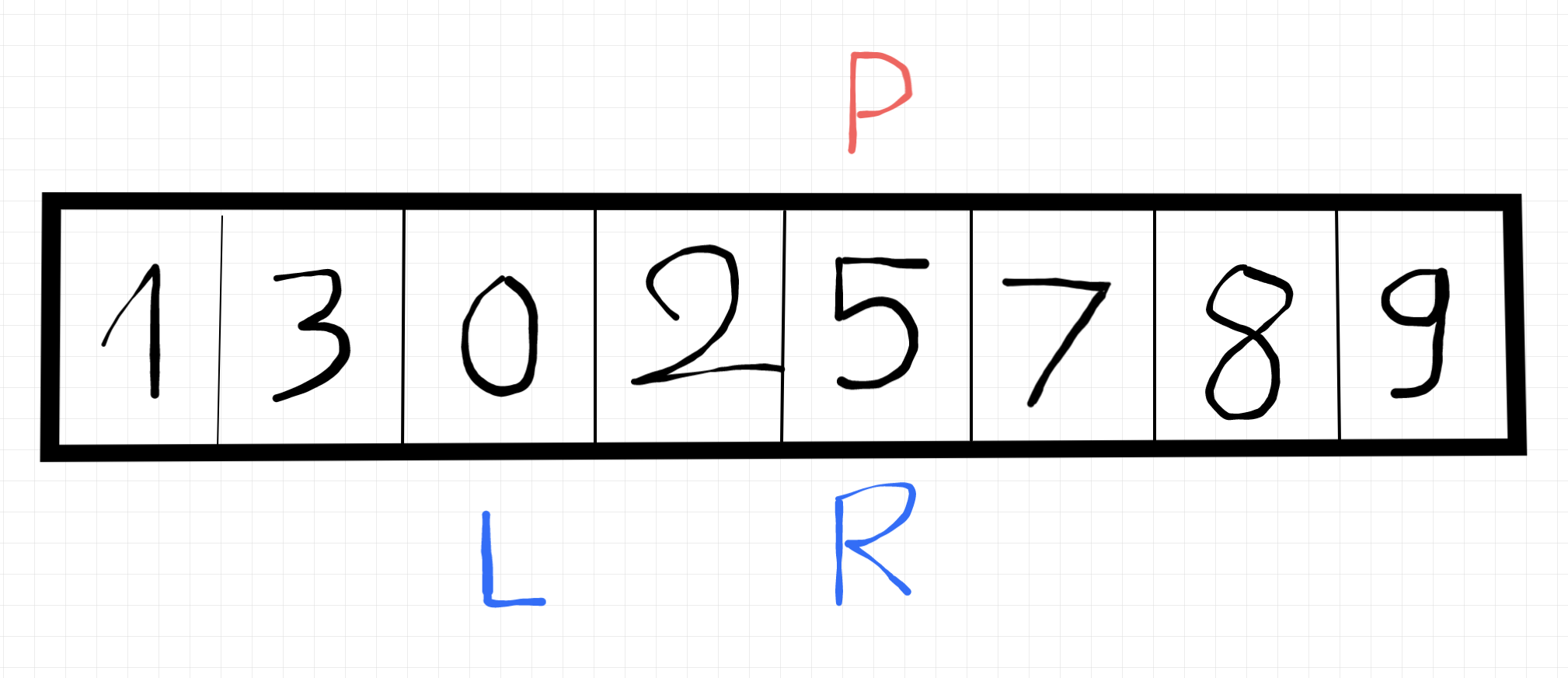
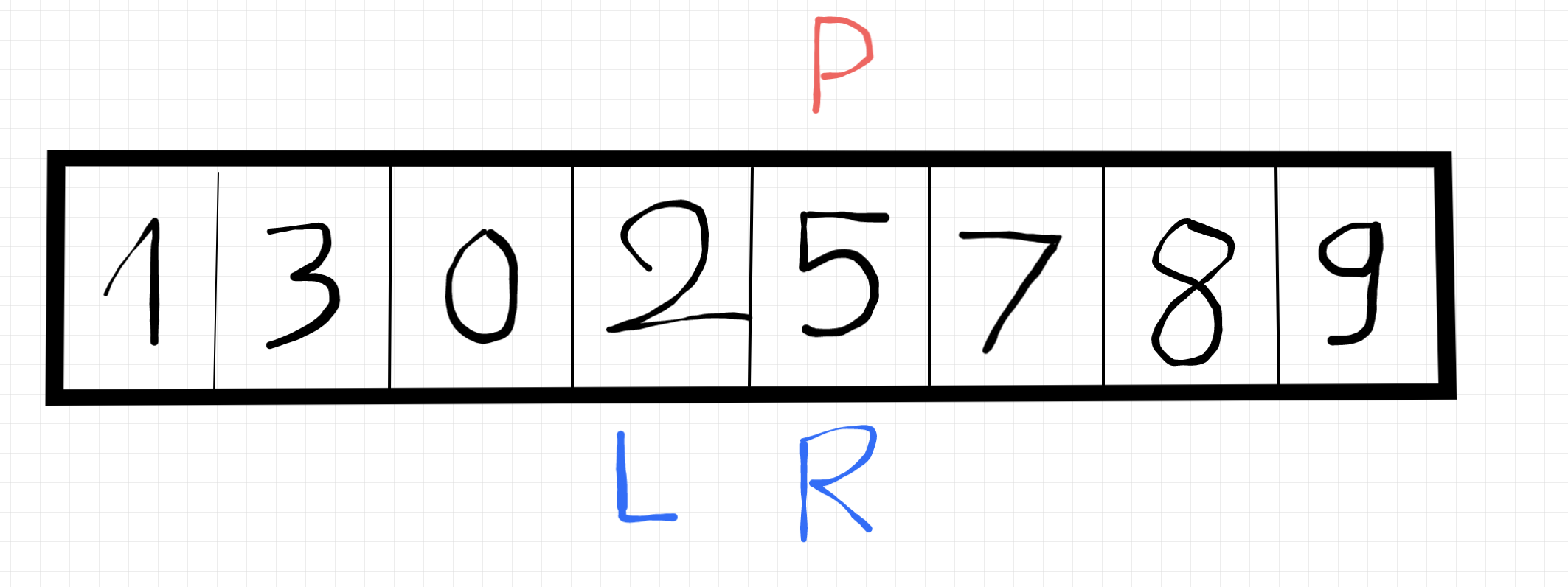
(không lời)

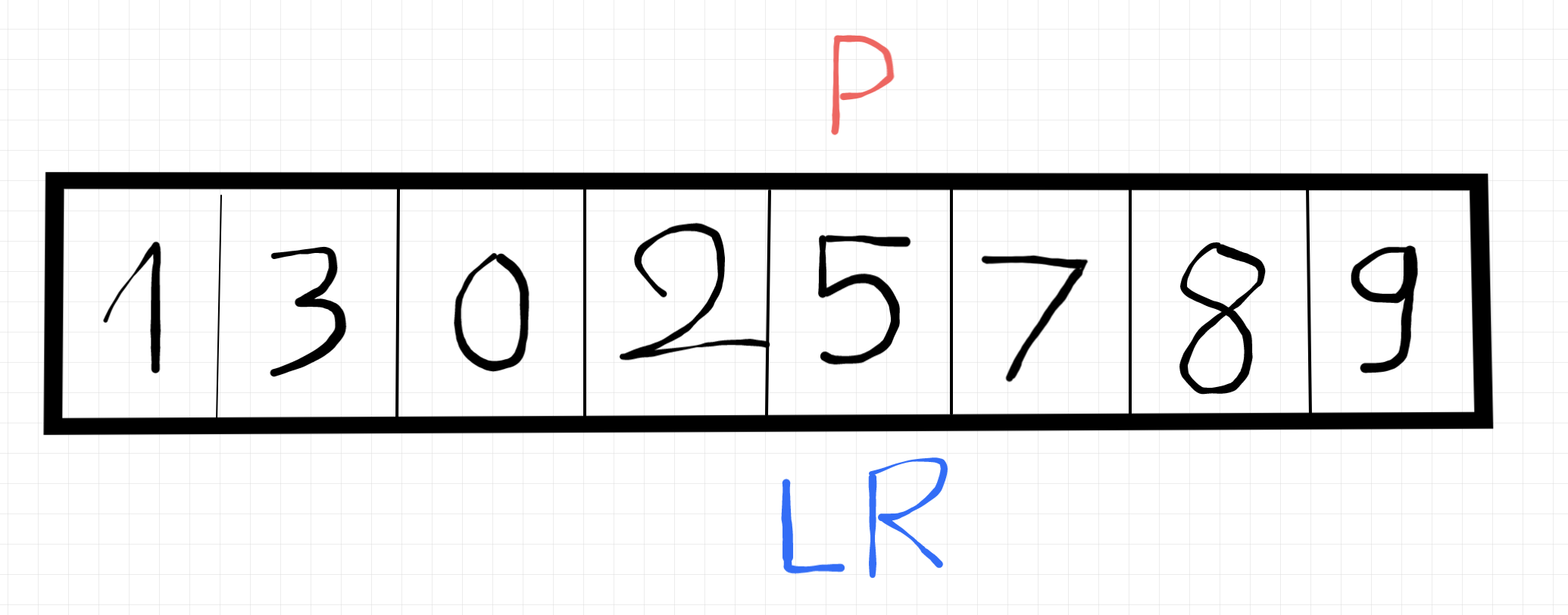
Lúc này left và right và pivot đã ở 1 chỗ rồi đó. Điều này có nghĩa là pivot đã nằm đúng vị trí của nó trong mảng cần sắp xếp 🤩.

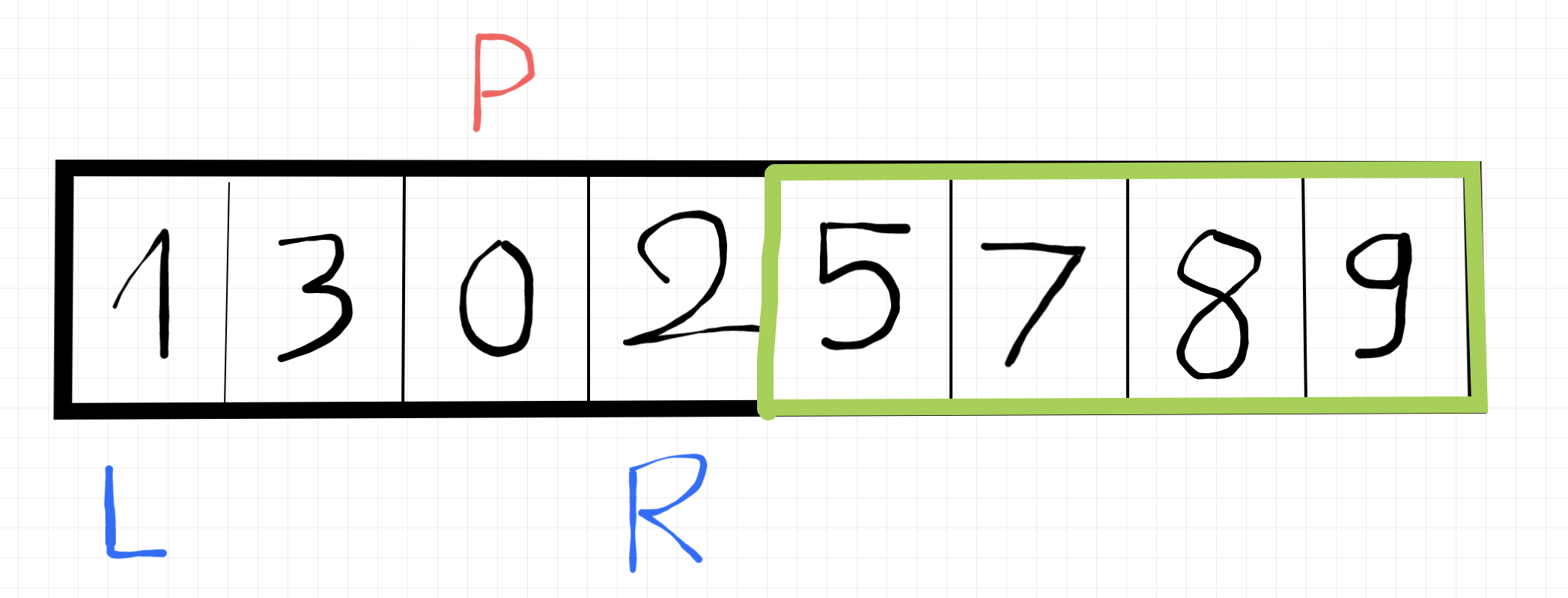
Cùng xem lại hen, Lúc này tất cả phần tử bên trái pivot đã nhỏ hơn so với pivot, và bên phải đã lớn hơn so với pivot. Và pivot đã chia mảng ban đầu thành 2 mảng con. Như ta thấy ở đây mảng bên phải đã được sắp xếp đúng, nên sau đó ta sẽ tiếp tục lặp lại các bước ở trên với mảng bên trái nhé. Để kiểm tra bạn có thuộc các bước chưa tui sẽ hem giải thích bằng lời nữa đâu á 👌. À khoan vì tui thích chon pivot ngẫu nhiên nên pivot của mảng con sẽ là số 0 😎. Tiếp đó nha.

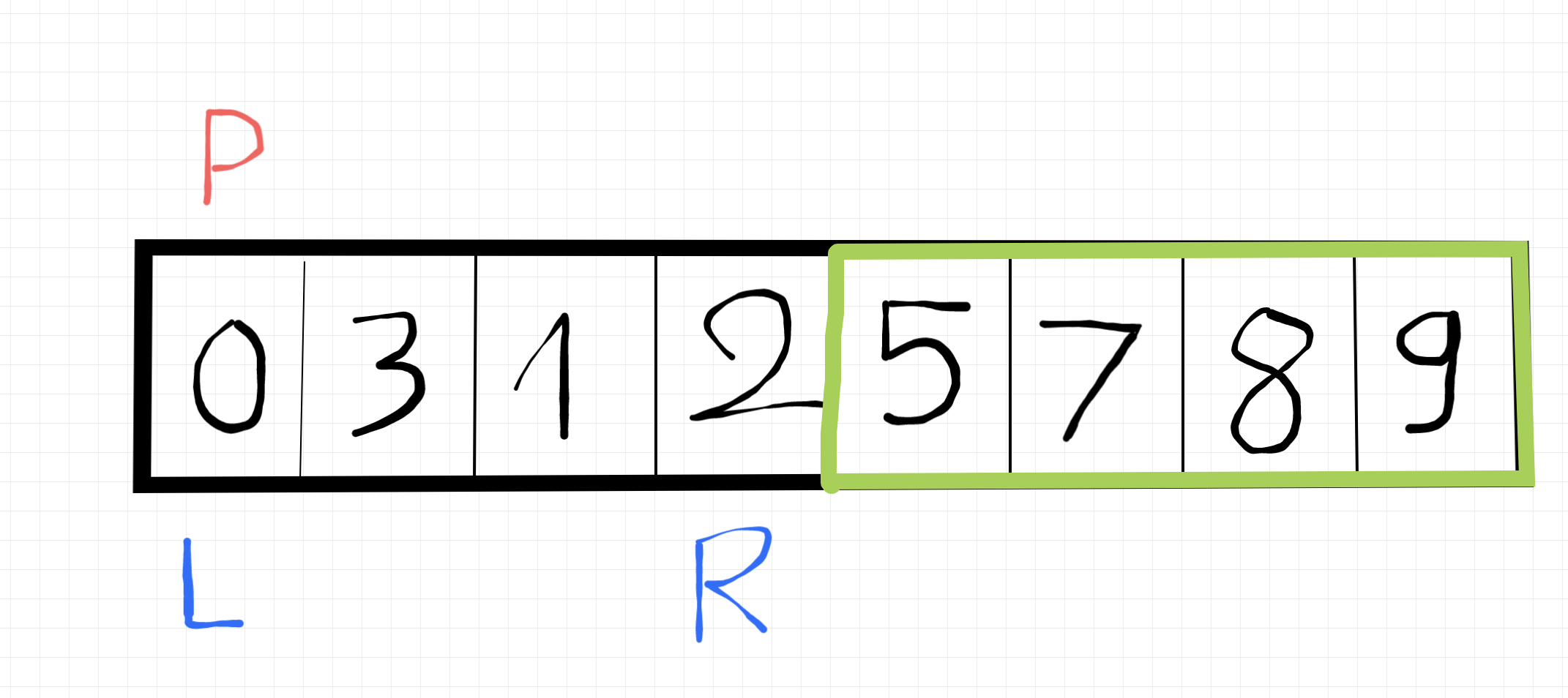
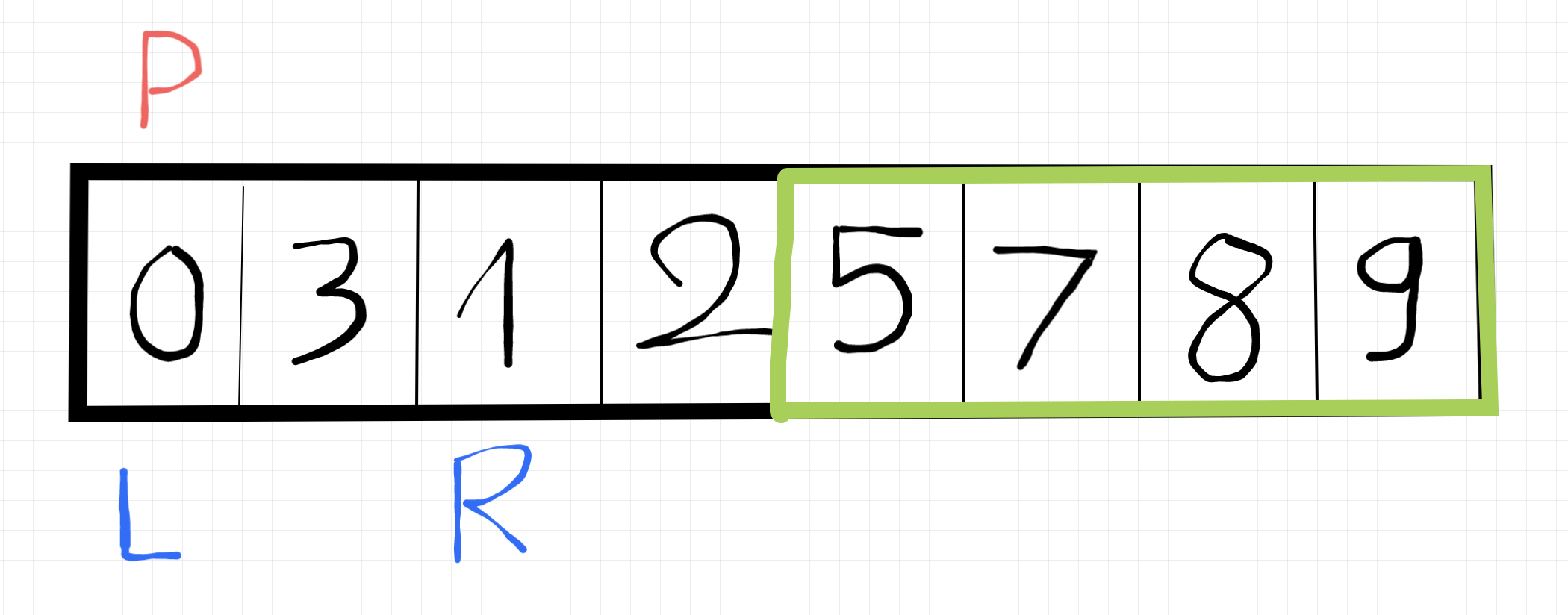
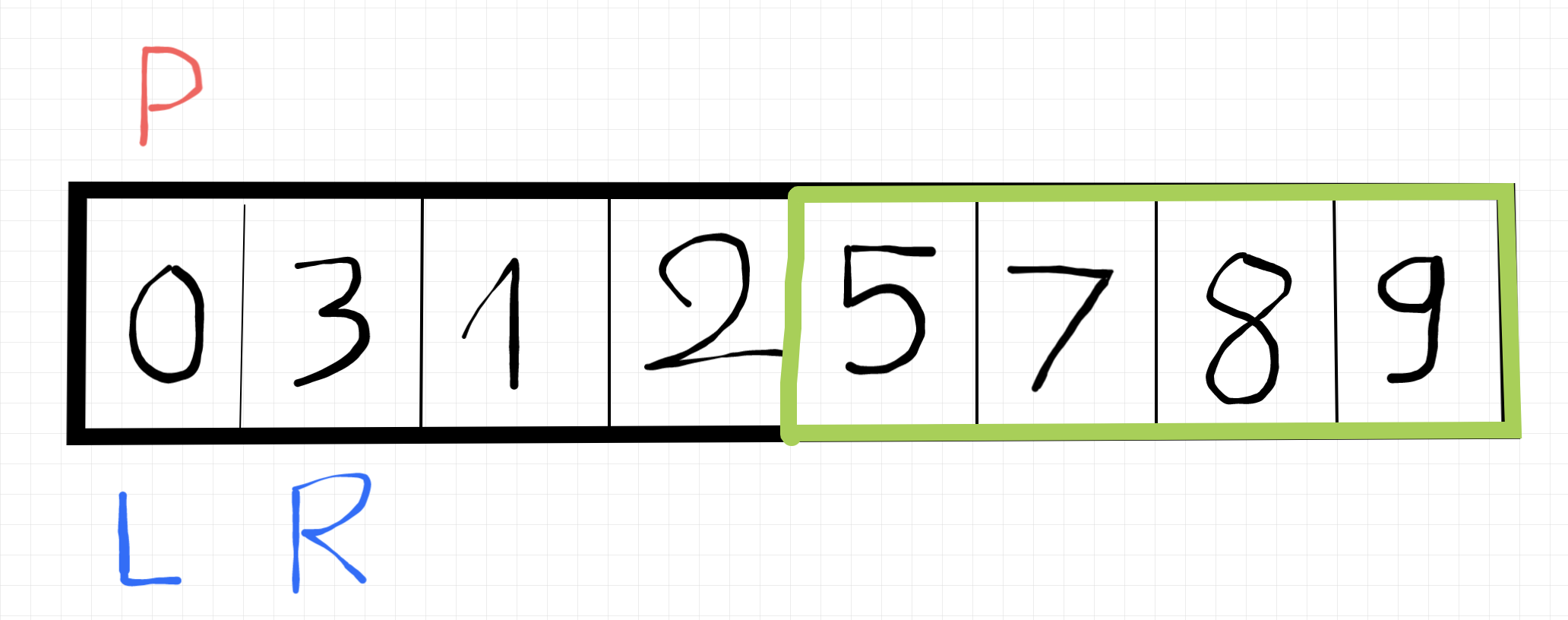
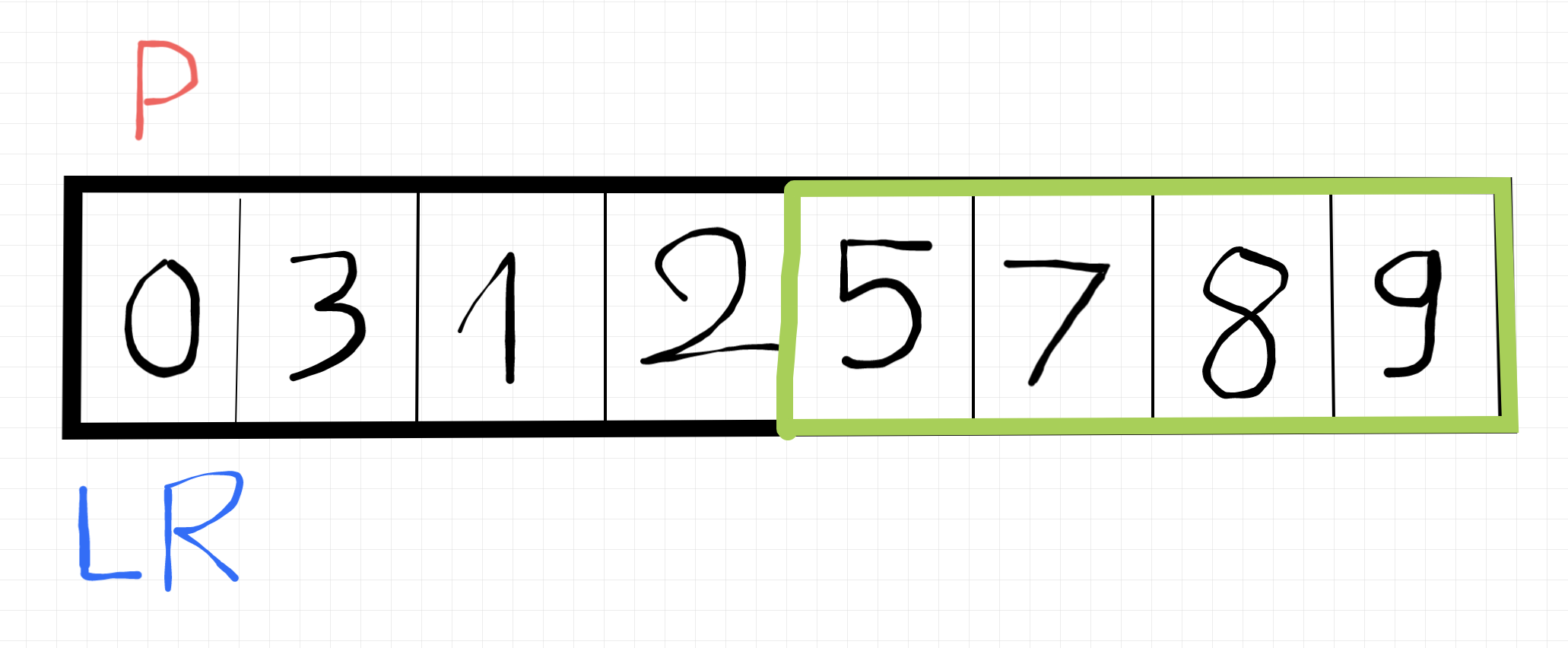
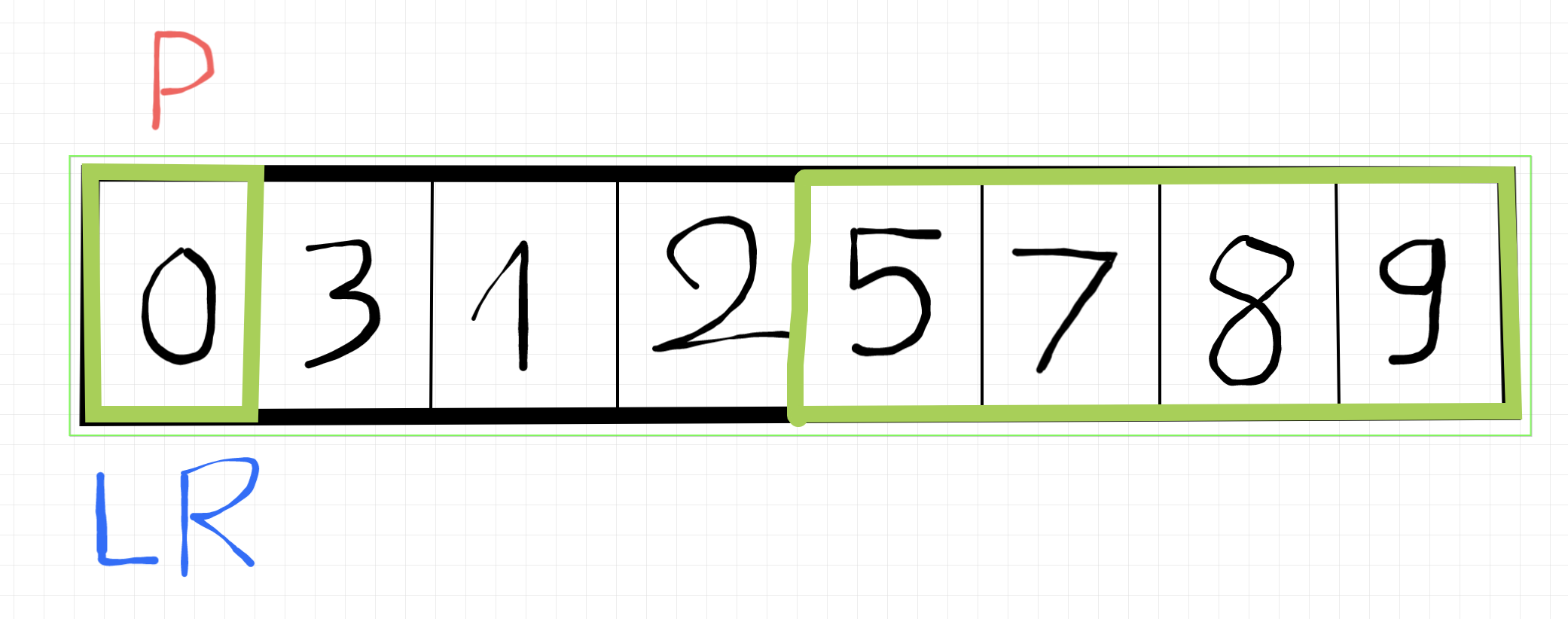
Dừng lại thôi vì pivot, left, right đã nằm chung một chỗ rồi. Lúc này số 0 đã nằm đúng vị trí sau khi sort rồi á, nên sau đó nó vẫn chia mảng này thành 2 mảng nhỏ, bị cái là số 0 nằm ở vị trí đầu tiên nên sẽ không có mảng nào nhỏ hơn nó nữa

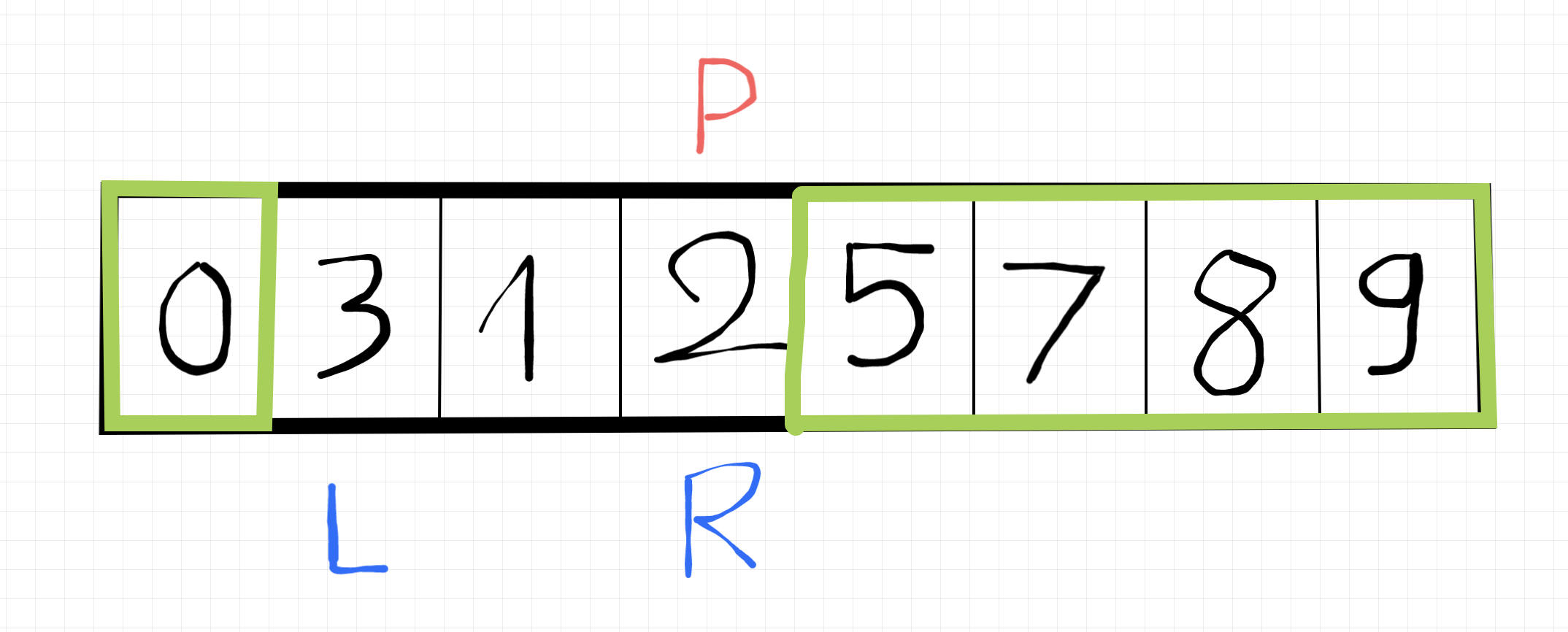
Vậy là chỉ còn 3 phẩn tử nữa thôi 🥸. Chọn pivot là 2.

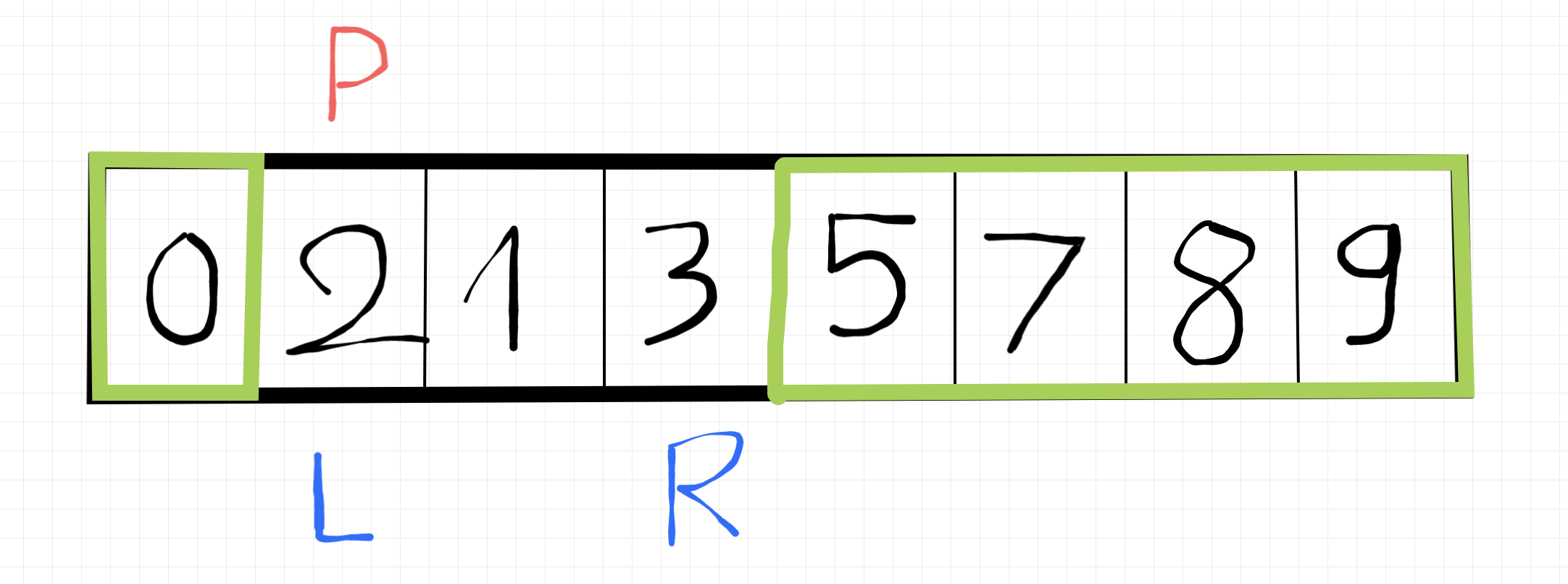
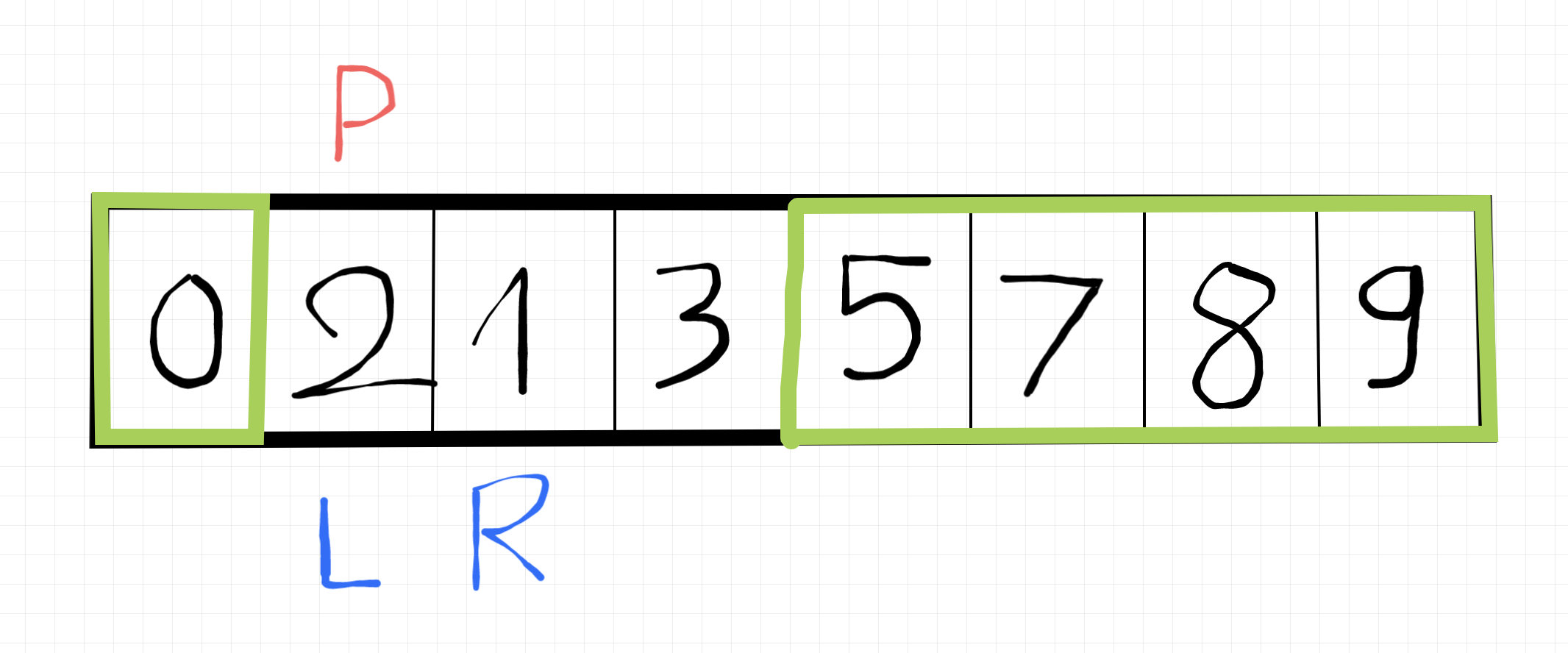
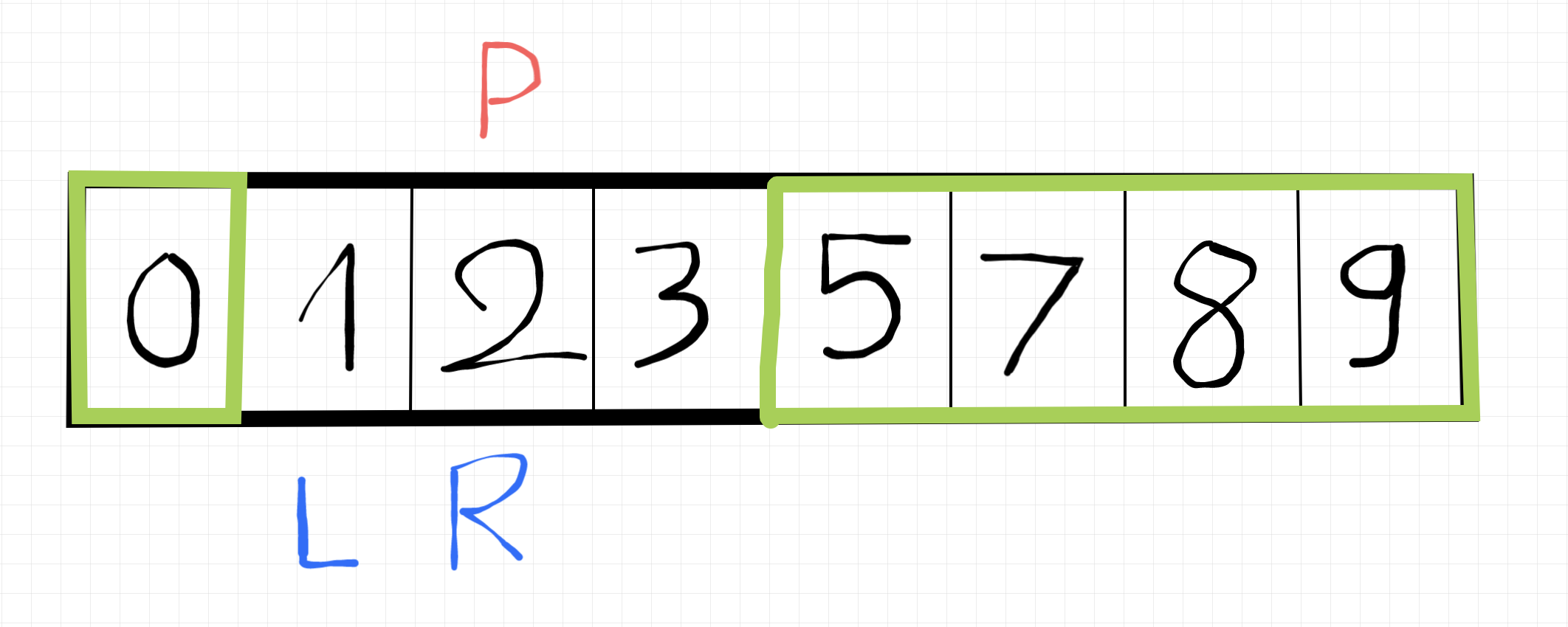
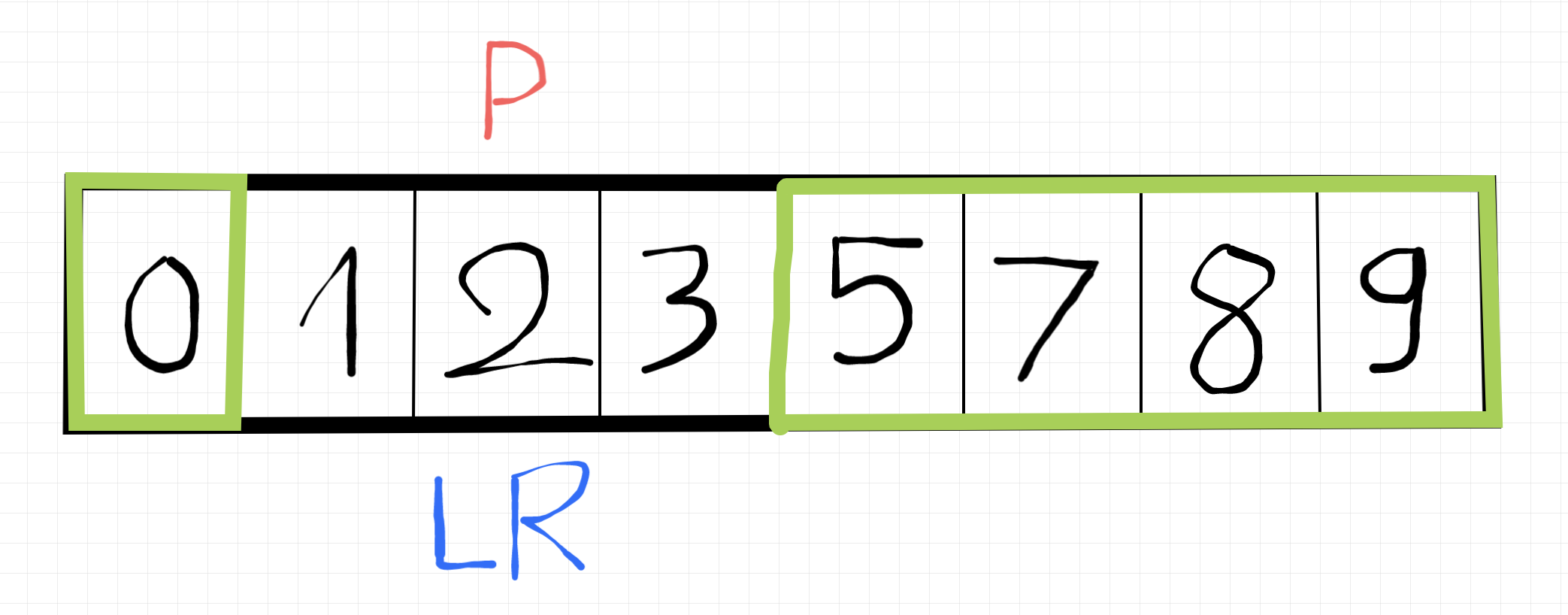
Xong rồi kìa, dễ chưa (hehe).

Time Complexity và Space Complexity

Như mình đã nói ở trên đây là một trong những thuật toán sắp xếp nhanh và hiệu quả nhất, nên Time và Space Complexity rất ổn nhen 💯.

Time Complexity của thuật toán QuickSort là O(nlog n) trong trường hợp trung bình và trong trường hợp xấu nhất. Trong trường hợp tốt nhất, thời gian chạy của thuật toán QuickSort là O(nlog n).

Không gian cần thiết để thực hiện thuật toán QuickSort là O(log n), và trong trường hợp trung bình và trong trường hợp xấu nhất. Trong trường hợp tốt nhất, không gian cần thiết là O(n).

Code Như thế nào?

Vậy là chung ta đã hiểu được ý tưởng chính của thuật toán này rồi nhỉ? Tiếp theo chúng ta sẽ cùng nhau thực hiên nó nhen.

def quick_sort(array,left=0,right=nil)
  right = array.length - 1 if right == nil
  return array if left >= right # Done sorting

  pivot = rand(array.length)
  #split array right higher/lower than pivot
  (pivot+1..right).each do |index| 
    if array[index] < array[pivot]
        temp = array[index]
        array[index] = array[pivot+1]
        array[pivot+1] = array[pivot]
        array[pivot] = temp
        pivot+=1
    end
  end  
  # recursive cases
  quick_sort(array,left,pivot-1) # lower than pivot
  quick_sort(array,pivot+1,right)  # higher than pivot
  
  return array
end

puts quick_sort([9,3,7,2,5,1,8,0])

Còn đây là bản ngắn gọn hơn :)

def quick_sort(array)
	return array if array.length <= 1

	pivot = array.delete_at(rand(array.length))
	# split array right higher/lower than pivot
	left, right = array.partition { |el| el < pivot }
  
	# recursive cases and merge
	return *quick_sort(left), pivot, *quick_sort(right)
end

puts quick_sort([9,3,7,2,5,1,8,0])

Kết

Chúng ta đã cùng nhau tìm hiểu quick sort là gì, ý tưởng chính và cách để implement nó hen, tất nhiên nó vẫn là 1 thuật toán cực kỳ cơ bản, nhưng cơ bản đối với mình chính là nền tảng á nha <3.

Mình quyết tâm viết lại vì dạo này mình nhận ra là mình quên nhiều thứ quá, vậy nên mình nghĩ đây cũng là một cách tốt để mình tìm lại các kiến thức xưa cũ 😌, chia sẻ cũng là một cách để học, biết đâu có ai đó lại giúp chỉ ra cái sai của mình thì sao ❤️. Và mình cũng sẽ không chỉ viết mỗi các vấn đề về giải thuật nữa, mà mình sẽ chia sẻ nhiều hơn (nếu mình biết) về những thứ khác nữa á.

Thực ra ai cũng có sai lầm và mình cũng vậy á, nên là nếu có sai sót mình rất mong được nghe các lời góp ý và chỉnh sửa của mọi người á, mình xin cảm ơn ✌🏻✌🏻.